Impressing Tog Even More...

By Gerd Waloszek

In the previous UI Design Issues column, I presented Fitts' law and told you that Tog (Bruce Tognazzini from the Nielsen Norman Group) likes to query job applicants for it. In this column, I want to expand on that, enabling you to impress Tog even more – provided that you did not fail the first test. I will present two other "classics:" Hick's law and the power law of practice.

Hick's Law

Hick's law deals with the time needed to choose between alternatives of equal probability. Originally, the law was targeted at simple motor decisions, such as hitting a number key on a numerical keypad or hitting a "yes" or "no" button in a psychological experiment. In short, Hick's law says:

Given n equally probable choices, the average time required to choose among them is approximately proportional to the logarithm to the basis 2 of the number of choices plus one.

That sounds rather hard to understand. Somewhat oversimplified, one might say:

The reaction time increases with the number of choices but at a considerably slower rate (namely, at a logarithmic one)

By the way, the "plus one" is due to the fact that a decision about "no key" is also a decision. Again, I do not want to bother you with the exact formula. You can find it, together with more details, in Wikipedia. Hick's law is similar in form to Fitts' law because both laws have roots in information theory. An intuitive argument for the logarithmic form of Hick's law is that people subdivide the total set of choices into binary categories: At each step, they eliminate about half of the remaining choices one by one, which would require a linear amount of time (from Wikipedia, adapted).

Example:

# Choices	1	2	3	7	15
Relative Time	1	1.6	2	3	4

Table: Relationship between time and number of choices

Applying Hick's Law

As already mentioned, Hick's law can be applied to hitting keys on a keyboard, where each key has the same probability of being a target. Hick's law is sometimes also used to justify menu designs. However, applying the model to menus must be done with care: The order of the commands plays an important role as to which strategy people use. For example, to find a given word in a randomly ordered word list – in this case, the name of a command in a menu – requires each word in the list to be scanned. This strategy consumes linear time; Hick's law does not apply here. Whereas, if the list is in alphabetical order, users may use a subdividing strategy and need only logarithmic time (from Wikipedia, adapted).

The Power Law of Practice

The power law of practice states that

When performing a task based on practice trials, people improve in speed at a decaying exponential rate *)
Or: The time needed for a particular task decreases proportional to the number of practice trials taken raised to a power of about -0.4
Or: The logarithm of the time needed for a particular task decreases linearly with the logarithm of the number of practice trials taken (this formulation is for the math geeks...)

*) I found this formulation in the UsabilityFirst glossary. Personally, however, I would not characterize such a decay as an exponential. For me one, "exponential" means a decay by the same factor for each time step (for example, 1/2, 1/4, 1/8, etc.), that is, not "n to the power of a constant" but "a constant to the power of n."

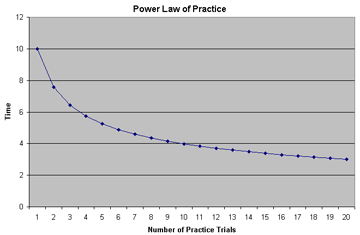
The power law of practice can be visualized as a learning curve or "the learning curve effect on performance" see figure 1).

Figure 1: The power law of practice shown as a so-called learning curve

Regrettably, Wikipedia's article on the power law of practice is incomplete, but there are other sources on the Web, such as the UsabilityFirst glossary, where you can find the formula and some details.

Applying The Power Law of Practice

The quantitative statement of the power law of practice has been applied to a wide variety of different human behaviors: immediate-response tasks, motor-perceptual tasks, recall tests, text editing, and more high-level, deliberate tasks such as game-playing (from University of Michigan, Artificial Intelligence Laboratory: Power law of Practice, adapted).

Because of the decay according to a power function, we can make two observations:

The largest improvements in speed are made during the very first trials. Therefore, we should be careful with generalizing timing results from first-time users.
The learning process lasts virtually endlessly. With workers who rolled cigars, small improvements could be demonstrated even after tens of thousands of trials.

A Word of Caution...

Please note, that typical reaction times at the computer are the result of a complex interplay of different, often competing, influences – Hick's law and the power law of practice are just two of them.

References

Wikipedia: Hick's law
Wikipedia: Power law of practice (incomplete article)
UsabilityFirst glossary: www.usabilityfirst.com/glossary/term_267.txl
Power Law of Practice (University of Michigan, Artificial Intelligence Laboratory): ai.eecs.umich.edu/cogarch0/common/theory/powerlaw.html
More references can be found in the above-mentioned articles

Originally Published: 07/11/2006 - Last Revision: 10/31/2009